8598. Волшебники и
волки
Однажды, прогуливаясь, Вы встретили n волков. У
каждого волка есть свой параметр силы – здоровье. При встрече с волками, у i-го
волка было hi единиц здоровья. Если у какого-то волка
здоровье падает до 0 или ниже, то он умирает.
К счастью вы волшебник, который может создавать
взрывы. Этими взрывами вы можете уменьшать здоровье волков. Одним взрывом
здоровье волков можно уменьшать следующими способами:
Выбрав какого-либо живого волка, вы производите взрыв
рядом с ним. В таком случае здоровье выбранного волка уменьшается на a единиц,
а всех остальных на b единиц. Значения a и b даны
Вам изначально.
Какое минимальное количество взрывов нужно произвести,
чтобы убить всех волков?
Вход. Первая
строка содержит три числа n (1 ≤ n ≤ 105),
a и b (1 ≤ b < a ≤ 109). В
каждой из следующих n строк задано число hi (1 ≤
hi ≤ 109) – здоровье i-го волка.
Выход. Выведите
минимальное количество взрывов, необходимых для уничтожения всех волков.
Пояснение. Тест
1. Создадим взрыв рядом с волком со здоровьем 8. После взрыва здоровье
у волков будет соответственно 3, 4, 1, -1. Второй взрыв
произведем рядом с волком со здоровьем равным 4. После второго взрыва все
волки умрут.
Тест 2. Чтобы
убить всех волков, надо рядом с каждым из них произвести 2 взрыва, в
итоге 4 взрыва. Меньшим числом взрывов убить всех волков невозможно
|
Пример входа 1 |
Пример выхода 1 |
|
4 5 3 8 7 4 2 |
2 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
2 10 4 20 20 |
4 |
|
|
|
|
Пример входа 3 |
Пример выхода 3 |
|
7 1 2 24 35 40 68
72 99 103 |
12 |
РЕШЕНИЕ
бинарный поиск
Анализ алгоритма
Пусть все волки могут быть убиты x взрывами. Это значит, что взрывы следует производить
возле тех волков, здоровье которых больше b * x. Уменьшение здоровья на a единиц мы рассматриваем как уменьшение здоровья на b, а потом еще на a – b единиц. Тогда количество взрывов, которое следует
произвести рядом с
i-ым волком
со здоровьем hi при hi > b * x, равно ![]() .
.
Действительно, пусть изо всех x совершенных
взрывов возле i-го волка будет совершено p взрывов. После чего i-ый волк будет убит. Тогда число взрывов не около i-го волка равно x – p и имеет место неравенство:
hi
≤ a * p + b * (x – p)
Решим это неравенство относительно p. Имеем:
hi
≤ a * p + b *
x – b * p;
hi
– b
* x ≤ p * (a – b);
![]()
Наименьшее целое значение p равно  .
.
Пусть функция canBeKilled(x) возвращает 1, если все
волки могут быть убиты x взрывами. Это
возможно тогда, когда (суммирование идет по тем значениям i, для которых hi > b * x)
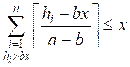
Для решения
задачи следует найти наименьшее x, для которого canBeKilled(x)
= 1. Это можно сделать при помощи бинарныого поиска, выбрав в качестве
начального интервала x ∈ [1; 109].
Пример
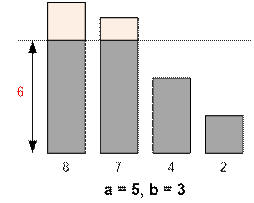
Рассмотрим
первый пример. Имеем: a = 5, b = 3. Всех волков можно убить 2 взрывами. Тогда здоровье всех
имеющихся четырех волков при двух взрывах уменьшится на 3 * 2 = 6
единиц. В остатке еще имеется 2 взрыва по a – b = 2 единиц,
которые следует направить на тех волков, здоровье которых больше 6.
Реализация алгоритма
В массиве h будем хранить здоровье волков.
#define MAX 100001
int h[MAX];
Функция canBeKilled(x) возвращает 1, если все
волки могут быть убиты x взрывами.
Округление сверху реализуем при помощи формулы
![]() = (x + y – 1) / y
= (x + y – 1) / y
int canBeKilled(int x)
{
long long res = 0;
for (int i = 0; i < n; i++)
if (h[i] > 1LL * x * b)
res += (h[i] - 1LL * x * b + a - 1) / a;
return res <= x;
}
Читаем входные данные.
scanf("%d %d %d", &n, &a, &b);
a -= b;
for (i = 0; i < n; i++)
scanf("%d", &h[i]);
При помощи бинарного
поиска вычисляем наименьшее количество взрывов, которыми можно убить всех
волков. Изначально это количество находится на промежутке [left; right]
= [1; 109].
left = 0;
right = 1000000000;
while (left < right)
{
mid = (left + right) / 2;
Если всех волков можно
убить mid взрывами, то продолжаем поиск
ответа на промежутке [left; mid]. Иначе продолжаем
поиск на промежутке [mid + 1; right].
if (canBeKilled(mid)) right
= mid;
else left = mid + 1;
}
Выводим ответ.
printf("%d\n", left);